一、准确度与精密度

1、准确度与误差

例1：测定酒精溶液中乙醇含量为

（1）50.20%；

（2）50.20%；

（3）50.18%；

（4）50.17%

平均值：50.19%，真实值：50.36%

什么是误差：分析结果与真实值之间的差值。

误差的表示：误差（E）= 测得值（X）- 真实值（T）

                  测得值(X) - 真实值(T)

相对误差（RE）=                           ×

                         真实值(T)

误差：表示测定值与真实值之差。

相对误差：误差在真实值（结果）中所占百分率。

有关真实值：实际工作中人们常将用标准方法通过多次重复测定所求出的算术平均值作为真实值。

准确度：实验值与真实值之间相符合的程度，误差越小，准确度越高；误差越大，准确度越低。

例2：测定值57.30，真实值57.34。

误差（E）= X – T = 57.30 - 57.34 = -0.04

                  E               -0.04

相对误差（RE）=       ×  =         × = -0.07%

                  T               57.34

例3：测定值为80.35，真实值85.39。

E = X – T = 80.35 - 85.39 = -0.04

      E             -0.04

RE =      ×  =       ×  = -0.05%

      T              80.39

得出结论：误差相同，但相对误差不同。

练习：测定值：80.18%，真实值：80.13%。

计算：误差（E），相对误差（RE）

应用：实际测定时，相对误差使用较多，仪器分析使用误差较多，具体情况具体分析。

2、精密度与偏差

例1：   甲         乙          丙

        50.20     50.40      50.36

        50.20     50.30      50.35

        50.18     50.25      50.34

        50.17     50.23      50.33

平均值：50.19     50.30      50.35

真实值：50.36

什么是偏差：表示几次平行测定结果相互接近的程度。

（1）偏差的表示：偏差（d）= X—X

                  d           X - X

相对偏差（d%）=     × =       ×

                  X             X

偏差：单项测定与平均值的差值。

相对偏差：偏差在平均值所占百分率或千分率。

精密度是指相同条件下几次重复测定结果彼此相符合的程度。

精密大小由偏差表示，偏差愈小，精密度愈高。

实际工作中：平均偏差的使用较普遍。

（2）平均偏差：是指单项测定值与平均值的偏差（取值）之和，除以测定次数。

                   | d₁| + | d₂| + | d₃| + …|d_n|      ∑ | di |

平均偏差d =                                  =            

                           n                         n

                     d              ∑ | di |

相对平均偏差（%）= —— ×   =             ×

                     X                 nX

例2：55.51，55.50，55.46，55.49，55.51

计算：X，d，d%  （见书P215页）

（3）标准偏差S：

相对标准偏差 = S/ X×

总结：在一般分析中，通常多采用平均偏差来表示测量的精密度。而对于一种分析方法所能达到的精密度的考察，一批分析结果的分散程度的判断以及其它许多分析数据的处理等，采用相对标准偏差等理论和方法。用标准偏差表示精密度，可将单项测量的较大偏差和测量次数对精密度的影响反映出来。

例3：甲：0.3，0.2，0.4，-0.2，0.4，0.0，0.1，0.3，0.2，-0.3

乙：0.0，0.1，0.7，0.2，0.1，0.2，0.6，0.1，0.3，0.1

计算：*组和第二组即甲组和乙组的d和S

                ∑ | di |

*组：d₁ =           = 0.24

                    n            

                ∑ | di |

第二组：d₂ =             = 0.24

                     n            

*组：S₁ = 0.28      S₂ = 0.34

由此说明：*组的精密度好。

3、准确度与精密度的关系（总结）

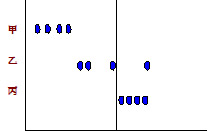
由甲、乙、丙三人的实验数据分析结果：（标准值为0.31）

甲：精密度很高，但平均值与标准样品数值相差很大，说明准确度低。

乙：精密度不高，准确度也不高。

丙：精密度高，准确度也高。

准确度高必须精密度高，精密度高并不等于准确度高。

二、误差来源及消除方法

    产生误差的原因很多，一般分为三类：系统误差、偶然误差和过失误差。

1、系统误差：由某种固定原因所造成的误差，使测定结果系统偏高或偏低。当重复进行测量时，它会重复出现。

①仪器误差：由于使用的仪器本身不够受造成的。

例：未经过校正的容量瓶，移液管、砝码等。

②方法误差：由分析方法本身造成的。

例：重量分析中由于沉淀的溶解、共沉淀现象。

滴定分析中，干扰离子的影响，等当点、突跃范围和滴定终点不符合。

③试剂误差：由于所用水和试剂不纯造成的。

④操作误差：由于分析工作者掌握分析操作的条件不熟练，个人观察器官不敏锐和固有的习惯所致。

2、偶然误差：由于在测量过程中，不固定的因素所造成的。有称不可测误差、随机误差。

例如：样品处理时微小的差别，气温、气流等环境因素。

偶然误差在分析操作中是无法避免的。对于同一试样进行多次分析，得到的分析结果仍不*一致的原因为偶然误差。偶然误差难以找出确定原因，似乎没有规律，但如果进行很多次测定，便会发现数据的分布符合统计规律：讲解“误差的正态分布曲线”

①正误差和负误差出现的机会相等。

②小误差出现的次数多，大误差出现的次数少，个别特别大的误差出现的次数极少。

③在一定条件下，有限次测定值中，其误差的值不会超过一定界限。

过失误差：由操作不正确，粗心大意引起的误差，舍去所得结果。

    例如：加错试剂、溶液溅失等。过失误差在工作中是*可以避免的。

3、提高分析结果准确度的方法

（1）选择合适的分析方法

化学分析：滴定分析，重量分析灵敏度不高，高含量较合适

仪器分析：微量分析较合适

（2）减小测量误差

例如：在重量分析中，测量步骤是称重，这时就应设法减少称量误差。

例如：天平的称量误差在±0.0002克，如使测量时的相对误差在0.1%以下，试样至少应该称多少克？

                  误差

     相对误差 =             ×  （试样重即真实值）

                  试样重

                E      0.0002

     试样重 =      =          = 0.2g

               RE      0.1%

称重必须在0.2g以上，才可使测量时相对误差在0.1%以下。

（3）增加平行测定的次数、减小偶然误差。

一般要求在2~4次，一般为三次，既可以得到比较满意的结果。

（4）消除测量过程中的系统误差

①空白试验：指不加试样，按分析规程在同样的操作条件进行的分析，得到的空白值。然后从试样中扣除此空白值就得到比较可靠的分析结果。

②对照试验：用标准品样品代替试样进行的平行测定。

            标准试样组分的标准含量

校正系数 =                           

               标准试样测得含量

被测组分含量 = 测的含量 Х 校正系数

zui有效的消除系统误差的方法。

③校正仪器：分析天平、砝码、容量器皿要进行校正。

三、有效数字及运算法则

1、有效数字：实际能测量到的数字。在一个数中，除zui后一位数是不甚确定的外，其它各数都是确定的。

例1：读取滴定管上的刻度：

    甲：23.43ml    乙：23.42ml    丙：23.44ml    丁：23.43ml

2、有效数字中“0”的意义

例2： 1.0008，        43181         五位

          0.1000，        10.98%         四位

          0.0382，        1.98×10^-10      三位

          54              0.0040         二位

          0.05            2×10⁵          一位

          3600            100            不明

“0”在有效数字中可作为数字定位或有效数字双重作用。

总结：

①数字之间和小数点后末尾的“0”是有效数字；

②数字前面所有的“0”只起定位作用；

③以“0”结尾的正整数，有效数字位数不清。

说明：4.5×10³（2位）；4.50×10³（3位）；4.500×10³（4位）。

3、实际应用

例如：50mL酸式滴定管，10ml < V_测 <   50mL；V_测 < 10mL。

4、数字修约规则

“四舍六入五成双”→ 数字修约规则由科学技术委员会颁布。

例3：

28.175        28.18  

28.165        28.16

28.2645       28.3     

28.2501       28.3    

2.154546→2.15455 →2.1546→2.155→2.16不正确

          ↓正确

         2.15

总结：

①当尾数≤4时舍去；

    ②当尾数≥6时进位；

    ③当尾数＝5，5后无数，全部为零时前一位奇数进1位，前一位偶数不进；

    5后并非全部为零时则进1。

5、有效数字计算规则：

（1）加减法：保留有效数字的位数，以小数点后位数zui少的为准。误差zui大的为准。

例4：0.0121 + 25.64 + 1.05782 = ？

①先按修约规则→全部保留小数点的后二位；

②再计算；

③不允许计算后再修约。

0.01                         0.0121    

         25.64                        25.64      

      +   1.06                     +   1.05782

          26.71                       26.70992

正确                        不正确

（2）乘除法：保留有效数字的位数，以位数zui少的数为准。

例5： 0.0121×25.64×1.05782 = ？

0.0121×25.6×1.06 = 0.328（结果要求是三位）

                   =0.3283456

以相对误差zui大的为准。     

                     ±0.0001

0.0121    RE =             × 100％ = ±0.8％

                     0.0121

                    ±0.01

25.64     RE =           × = ±0.04%

                    25.64

     ±0.00001

1.5782   RE =             × = ±0.0009%

                     1.05782

6、自然数

例6：水的分子量 = 2×1.008+16.00=18.02

2≠有效数字，非测量所得是自然数，其有效位数为无限。